2025年非線性泛函分析及其應(yīng)用學(xué)術(shù)研討會

（2025年10月31日-11月2日）

報告摘要

Multiple solutions for nonhomogeneous Klein-Gordon-Maxwell system with Berestycki-Lions conditions

吳行平  西南大學(xué)

報告摘要：This paper is concerned with a kind of nonhomogeneous Klein–Gordon–Maxwell system? Δ u?(2 ω+ ?) ? u= g (u)+ h (x), in R 3, Δ ?=(ω+ ?) u 2, in R 3, where ω> 0 is a constant and g satisfies the Berestycki–Lions type conditions. By using Ekelands variational principle, the mountain pass theorem, Poho?aev identity and some new tricks, two nontrivial solutions can be obtained here

報告人簡介：西南大學(xué)教授，碩導(dǎo)，美國《數(shù)學(xué)評論》評論員。曾獲重慶市人民政府自然科學(xué)二等獎,和三等獎。1982年9月至1986年7月于西南師范大學(xué)數(shù)學(xué)系讀本科;1986年8月至1989年6月于西南師范大學(xué)數(shù)學(xué)系讀研究生;1989年6月獲碩士學(xué)位。1989年7月留校工作; 1992年晉升為講師; 1998年6月晉升為副教授; 2004年晉升為教授。主要研究領(lǐng)域是非線性泛函分析、非線性橢圓方程、二階Hamilton系統(tǒng)。發(fā)表論文多篇。

Li-Lin公開問題及相關(guān)研究

唐之韻 博士后（西南大學(xué)）

報告摘要： 2012年，Y.Y. Li 和 C.-S. Lin 提出了一個公開問題：當(dāng) 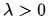 且 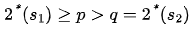 時，如下橢圓方程是否存在正解？(Arch. Ration. Mech. Anal. 203(3): 943-968, 2012)

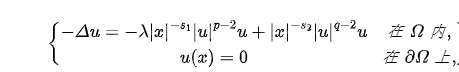
其中 是 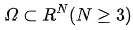為光滑有界區(qū)域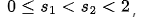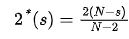， 為Hardy-Sobolev臨界指數(shù)。

我們通過研究，首次對該問題部分情形給出否定性結(jié)論，同時得到存在性結(jié)果；并拓展研究了兩類次臨界情形與一類無界區(qū)域情形，獲得正解存在性、分歧及非存在性等結(jié)論。

報告人簡介： 唐之韻，博士，2025年博士研究生畢業(yè)于中南大學(xué)，自2025年8月至今于西南大學(xué)數(shù)學(xué)博士后流動站從事研究工作。主要研究方向為非線性泛函分析及其在偏微分方程中的應(yīng)用。相關(guān)工作相繼發(fā)表在Calc.Var and PDEs, J. Differential Equations, Commun. Anal. Mech., J. Appl. Anal. Comput. 等雜志。

Ground state solutions for the nonlinear Schrodinger-Bopp-

Podolsky system with potentials

李麟   重慶工商大學(xué)

報告摘要：In this paper, we consider the following nonlinear Schrodinger-Bopp-Podolsky system. By using some new analytic techniques and new inequalities, we prove the above system admits a ground state solution under mild assumptions on potential V and nonlinearity f. Moreover, we also give a simple minimax characterization of the ground state energy.

報告人簡介：李麟，重慶工商大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院副教授，美國數(shù)學(xué)會特邀評論員。2015年西南大學(xué)獲理學(xué)博士學(xué)位，導(dǎo)師為唐春雷教授和沈自飛教授。主要研究方向為臨界點理論及其在微分方程中的應(yīng)用。曾在University of California, Irvine訪問，合作導(dǎo)師Martin Schechter教授。在《NA-TMA》、《NA-RWA》、《JMAA》、《TMNA》等雜志發(fā)表數(shù)篇論文。主持國家自然科學(xué)基金青年基金1項、重慶市科委自然科學(xué)基金1項、重慶市教委自然科學(xué)基金1項。

Multiplicity of normalized solutions for nonlinear Choquard equations

李貴東 貴州大學(xué)

報告摘要In this talk, we report our recent works about the existence of normalized solutions to Choquard equation. Under the general assumption of the nonlinear term F and within an appropriate mass range, we prove the existence and multiplicity of solutions to Choquard equation, which may manifest as global minimizer, local minimizer, or mountain pass-type solutions.

報告人簡介：李貴東，博士，碩士研究生導(dǎo)師，貴州大學(xué)特聘教授，美國數(shù)學(xué)會《Math. Review》評論員。研究方向為非線性泛函分析及其在偏微分方程的應(yīng)用，已在《J. Differential Equations》《Nonlinearity》《Nonlinear Anal.》等國際權(quán)威數(shù)學(xué)期刊發(fā)表 30 余篇論文，其中SCI一區(qū)論文 7 篇，二區(qū)論文 5 篇；目前主持國家青年基金等 3 項科研項目, 還擔(dān)任《Adv. Nonlinear Anal.》《J. Math. Anal. Appl》《Complex Variables and Elliptic Equations》《Communications in Nonlinear Science and Numerical Simulation》《Appl. Math. Lett.》《Qual. Theory Dyn. Syst》等SCI期刊審稿人。